資料處理流程(Process)

機器學習(Machine Learning)處理資料的生命週期(Life cycle) 與 Data Mining 是一致的，這方面有一個跨產業的標準，稱之為『CRISP-DM』(cross-industry standard process for data mining)，如下圖，分為六個步驟：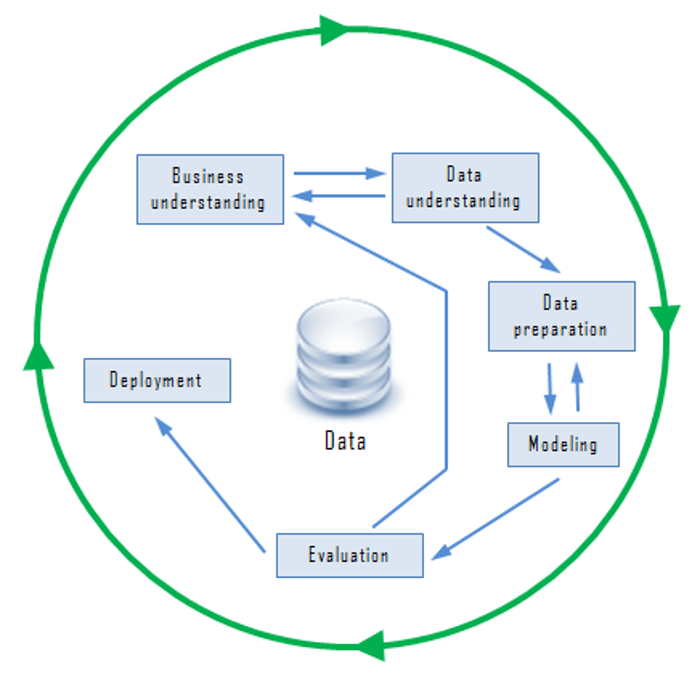

圖. CRISP-DM，圖片來源：『Data Mining Processes』

1. Business understanding：釐清商業目標及需求，訂定計畫目標，規劃如何從現狀到達目標的步驟。
2. Data understanding：有哪些資料? 從哪裡蒐集? 資料的品質是否達標?
3. Data preparation：這一階段的工作通常會佔整個專案90%的時間，資料經過篩選、清理(Clean)、統一格式(Format)、缺失值(Missing value)處理、轉換(Transform)，才會變成可用的資料集。
4. Modeling：決定哪一種或多種模型? 如何訂定測試場景，以驗證結果? 選用哪一種模型工具? 是否滿足所有利害關係人(Stakeholders)的需求?
5. Evaluation：評估是否符合商業目標? 資料挖掘的過程可能會產生新的商業需求，必須再回第一步驟，反覆實驗，最後再決定是否可以佈署到正式環境?
6. Deployment：佈署前、後，我們都會準備一個報告，說明整個專案過程獲得的成果，包括知識、如何應用以及專案獲得的經驗(Lessons learned)。
   ** 以上內容節錄自『Data Mining Processes』

Kaggle 是一個機器學習(Machine Learning)的競賽平台，網站上其實提供了許多的範例供競賽者參考，例如『Zillow EDA On Missing Values & Multicollinearity』就針對『房屋估價』給了一個很詳盡的分析流程，有興趣的讀者可以上網瀏覽，與 CRISP-DM 相互印證。

資料處理

從上面的流程，在『機器學習』專案執行時，有兩個主要的工具 -- Data 及 Model，之前，我們討論CNN/RNN/GAN...等 Neural Network 演算法都是從 Model 著手，如果 data 的品質也能提高，可以改善預測的準確度嗎? 是的，這就是『特徵工程』(Feature Engineering)的領域。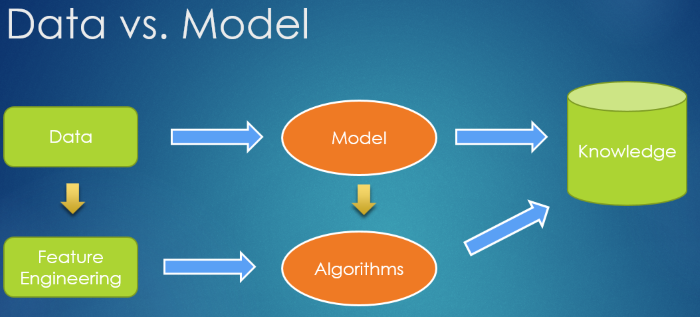

圖. Data vs. Model

我們看下圖，如果要將圖形上的點分為兩類(+、口)，左圖直接以簡單迴歸 y=ax+b，就可以很容易的切出一道分隔線，清楚區分兩類(+、口)，右圖『+』都集中在中間，也就是x與y呈現非線性的關係，可能是 y = ax*x + b (x平方)，這時，我們有兩個方法來解決，一種是模型改為 y = ax*x + b，另一種就是將 input 直接平方，模型維持原來的 y=ax+b，後者就是所謂的『特徵工程』(Feature Engineering)。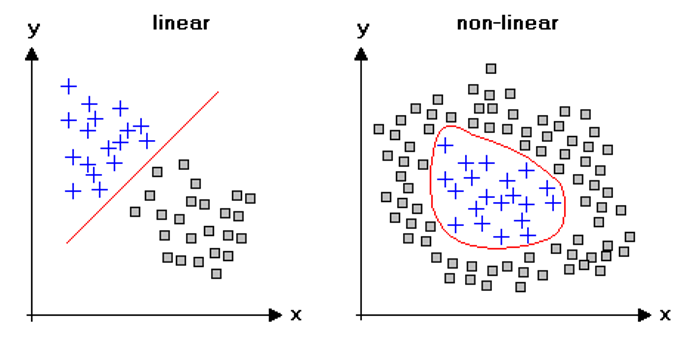

圖. 線性與非線性關係，圖片來源：Introduction to Data Mining with R

還有一種狀況我們會使用到『特徵工程』，就是特徵變數(x)很多時，而這些變數又互相關聯，例如，預測股價時，特徵變數考慮利率、匯率、景氣燈號、物價指數、公司營收...，其實，這些因素都是相互影響，建置模型時，通常假設變數間是獨立的，推導出來的模型必然與現實不合，反之從 data 著手，我們可以依貢獻度大小，篩選變數或將變數加工，是比較合理的方法，這種方法稱為『降維』(Dimensionality Reduction)，以下我們就來討論這個技術。

『降維』(Dimensionality Reduction)

降維就是減少特徵變數(x)的數量，主要分成兩類：

1. 特徵選取(Feature selection)：直接篩選部分變數，這種方式可能會遺漏重要資訊。
2. 特徵萃取(Feature extraction)：其實之前我們已做了很多了。
   • 語音：把頻率轉換成MFCC特徵向量，請參閱『Day 25：自動語音識別』。
   • 圖像：CNN將像素透過卷積轉換，將原始資料轉換成易於分析的特徵，請參閱『Day 06：卷積神經網路』。
   • 文字：自然語言處理時，我們也將單字轉為詞向量，請參閱『Day 13：自然語言處理』，再經過 t-sne 可轉為二維，顯示詞向量間的關係。
     
     圖. Word2vec向量空間，圖片來源：Google Open Source Blog

降維的演算法很多，分類如下：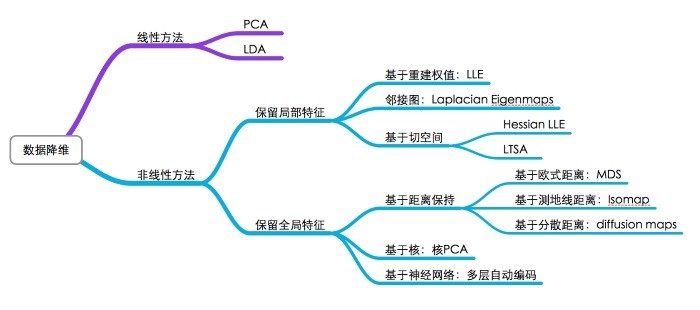

圖. 降維演算法的分類，圖片來源：SNE與t-SNE降維演算法理解

比較熱門的方式有兩個 -- 『主成分分析』(Principal Component Analysis，PCA) 及 t-SNE(t-Distributed Stochastic Neighbour Embedding)，我們來看看這兩個演算法的作法。

『主成分分析』(Principal Component Analysis，PCA)

『主成分分析』以各特徵變數的變異數(Variance)，作為貢獻度衡量的基準，愈大者貢獻度，另外，再依『共變異數』(Covariance) 度量所有變數的關聯性，與其他變數關聯性高的，且相對貢獻度較低者，就捨棄或予其他變數合併，希望降維之後，仍保有最大可能的資訊。

PCA 是一種線性降維的方式，如果特徵間的關聯是非線性關係，可能會導致擬合不足（underfitting）的情形發生，有些數據的集群會不夠明顯。

主成分分析在很多套件都有直接支援，我們看看程式如何處理：

from sklearn.decomposition import PCA
...
# iris.data : 輸入，n_components為主成分分析降維後的維度
PCA(n_components=2).fit_transform(iris.data)

t-SNE

t-SNE 為改善 PCA 的缺點，採取非線性的處理，將高維的資料假設為常態分配，低維的資料假設為自由度為1的t分配，以避免低維的資料受到變異數的影響，t分配的兩端尾部較厚，可避免低維全部擠在一起。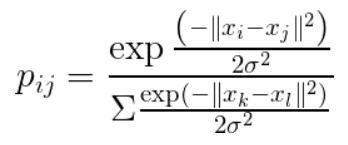

圖. PCA 2D 高維資料常態分配機率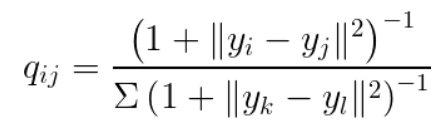

圖. 低維資料t分配機率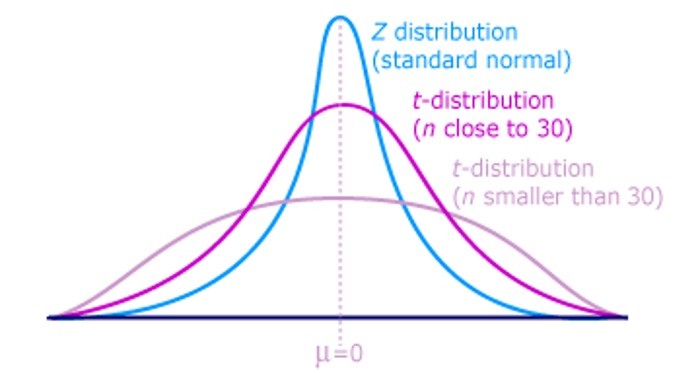

圖. t分配 vs. 常態分配，圖片來源：Statistical Sampling and Regression: t-Distribution
t-SNE的算法最優，但計算速度也較慢。我們看看下圖，PCA與t-SNE的2D投射效果，很明顯 t-SNE 分類效果較好。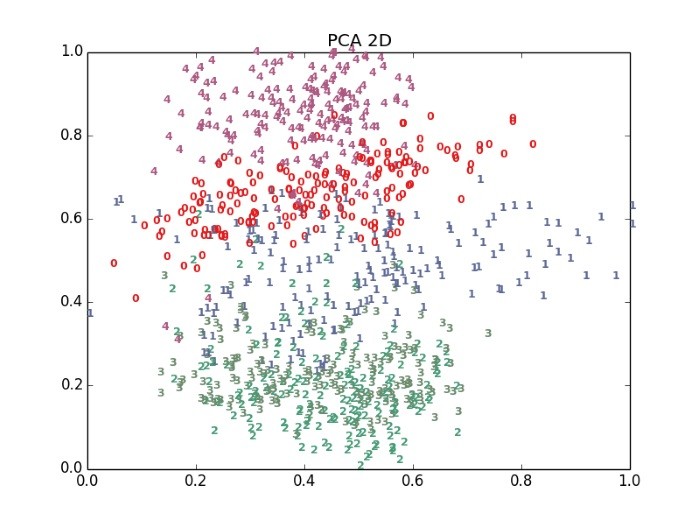

圖. PCA 2D 投射效果，圖片來源：流形學習-高維數據的降維與視覺化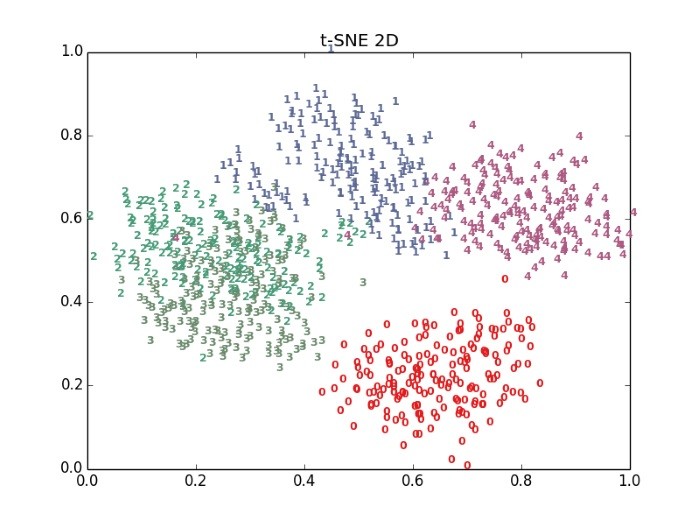

圖. t-SNE 2D 投射效果，圖片來源：流形學習-高維數據的降維與視覺化

t-SNE 在很多套件都有直接支援，我們看看程式如何處理：

from sklearn.manifold import TSNE
...
# x_std : 輸入，n_components：降維後的維度
tsne = TSNE(n_components=2, random_state=0)
x_std_2d = tsne.fit_transform(x_std)

我們看一個有趣的程式，它以t-SNE展示人臉辨識的相似度，如下圖，郭子乾多種模仿對象的相似度比較，郭子乾怎麼扮都與本人比較像，與模仿的對象距離較遠。

圖. t-SNE 相似度比較，圖片來源：t-sne-lab

結論

特徵變數過多，不降維有三個缺點：

1. 過度擬合 (overfitting)
2. 訓練速度慢
3. 如果超過三個特徵以上，不易視覺化
   因此，雖然 Neural Network 訴求能以 Generic Approach 解決問題，不要依賴各領域專家針對性的處理問題，但是原始資料(Raw data)的前置處理有時候還是需要『特徵工程』的協助。